I’m always delighted when a reader crawls out of the woodwork and says “hi”, even if it is to set me some maths homework. Kevin Stevens, author of the blog Flipyouforit (check out his brilliant Online Rounders parody) swelled my known audience last week to as many as five, and wrote:
I was wondering if I had a partner playing the HUP 4 man games on stars and we split the profit, would playing as a team give us any additional mathematical advantage?
Now I also know that at least two of my readers are maths teachers (that’s, what, 60% of them?) so I may be getting graded on this but here goes…
I’m assuming that you already feel you have an edge over the field, and therefore the question is whether a double entry will improve your edge, although it will also be interesting to see if this strategy affects a losing player or a break-even player.
Let’s say your probability of winning any given heads-up game is p (and therefore the probability of losing is 1-p). For simplicity, I’m assuming that both members of the team are equally skilled – or that one person is playing under two different accounts on two PCs.
The 4-man tournaments in question are two round, heads up shootouts with just one prize to be won. I’m going to assume a 10% entry fee on all buy-ins. So let’s say the buy-in amount is b, making the amount you pay to enter 1.1b and the prize pool 4b.
If you enter the tournament alone, your expected return is 4bp2 – the prize pool multiplied by the probability of winning both rounds.
We can use this value to find out what it takes to be a winning player. Your ER must be greater than the amount it costs to play, so with the 10% rake structure this is:
4bp2 > 1.1b
=> p2 > 1.1/4
=> p > 0.524
So to be a winner in this format, you have to win – on average – more than 52.4% of your games.
However, to be able to compare to the other strategy, which has several scenarios to consider, a more useful number to remember is the EV per dollar played, which is 4bp2/1.1b = 3.636p2
Let’s ignore the obvious ethical issues and say Bill and Ted are on the same team and Evil Bill and Evil Ted are your opponents on any given sit-and-go.
Statistically, the first round draw will throw up Bill vs Ted one-third of the time. When you’re playing against your partner, all that happens is you pay double to guarantee a seat in the final.
If you have an edge over the field, you’re losing out by not being able to play a meaningful game in this round. As one of the two players will always progress to the final, exactly 50% of your team will win. Therefore if you normally expect to win, say, 60% of heads-up encounters, this draw has reduced your variance but it’s also reduced your overall edge.
As you don’t need to play poker, you could spend the time studying the other two players which might give you some useful information to use in round two (or, if you think they are watching you, you could throw off some wonderful false information).
However, in terms of probabilities, your ER from the tournament when you draw your partner in round 1 is simply 4bp (prize pool multiplied by probablity of winning one round).
The other two-thirds of the time it wil be good vs evil in round 1, and this is where it gets interesting. One of three things can happen:
1. Good triumphs. Bill and Ted both win round 1 and you’re guaranteed to take all the money in the final.
Just like when you play each other in round 1, you’d rather be playing the final with an edge than splitting the money 50/50. However, when you’re both winning players you are each more likely to get to be in this situation than the evil robot dudes.
This part of your ER is 4bp2 (prize pool multiplied by probability both players of winning round one).
2. We only have one bodacious hero in the final. This part of your ER is 8bp2 – 8bp3.
Cubed probabilities, wtf? OK, let’s check it with Bully…
The probability of Bill winning and Ted losing in round 1 is p(1-p). We end up in the same situation if Ted wins and Bill loses so overall we’re looking at a probability of 2p(1-p) that we have just one hero in the final. When we get there the probability is p that we will win prize money of 4b.
Multiply it all together
2p(1-p) x p x 4b
=> 8bp2(1-p)
=> 8bp2 – 8bp3
I think.
3. Evil Bill and Ted both prevail and you’re boned.
This happens the rest of the time, and we win nothing so we don’t care.
Right so time to stick it all together.
Overall, your ER is
1/3(4bp) + 2/3(8bp2 – 8bp3)
Yuck. And don’t forget that this strategy costs 2.2b to play, so we need to divide by that to get the EV per dollar.
As we now have some expressions that are verging on the horrible (and, certainly, they’re horrible to type) it’s at this point I give up on the algebra and hand over to Mr Graph.
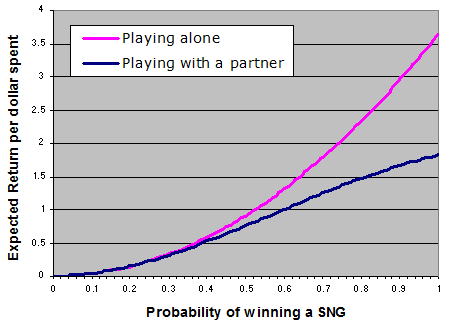
Excel hasn’t rendered the graph very smoothly, but you should get the idea. Unless you’re a particularly awful player, entering the tournament as a team reduces your overall edge. Not only that, but the better you are, the more dramatic the impact is.
For really large values of p, this stands to reason. If you could win every single game without fail, why would you ever play with a partner when you could scoop the prize money by paying just one buy-in instead of two.
However, what’s significant is that even if are an “average” player and win precisely half your games (p=0.5) you are better off going it alone than playing as a team.
It’s not that clear on the graph, but for low values of p, you’re slightly better off playing with a partner. It doesn’t turn you into a winner, but dollar-for-dollar you lose money a little less quickly. (You’ll spew more slowly with two entries in $5 tournament than you do with one entry in a $10).
You can just about see this if you zoom in really close.
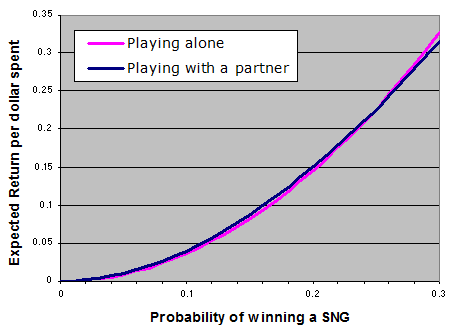
The magic number – the likelihood of winning which is good enough that you’re better off not playing with a partner – is 0.25. If you win 25% of encounters, it makes no difference whether or not you play yourself in round one and win a quarter of the finals, or if you just roll the metaphorical dice and win a quarter of all your games.
Let’s be honest though – if you can’t win one heads up game in four on average, you’d be better off playing roulette than trying to cheat at poker.
EDIT: Already found one error with my graphs. The “magic number” should be 0.5 not 0.25, although this does not affect the conclusion that this is a bad strategy.

Comments