There was a story in the news yesterday about a South Korean woman who had finally passed her written driving test on the 950th attempt.
It’s here if you missed it: http://news.bbc.co.uk/1/hi/world/asia-pacific/8347164.stm
This is a multiple choice test with a pass mark of 60%. I have to admit that my first thought was that, given nearly a thousand goes, I would be fairly confident about passing a test about anything under these conditions – even in if it was written in Korean.
Surely even the chance of fluking it is better than 1 in 950?
Well, apparently not – and significantly so.
I couldn’t remember the quick way to calculate this but fortunately Claire knew which buttons on the calculator did it, and she also found a web site that gave the same answer: http://stattrek.com/Tables/Binomial.aspx
It looks like this:
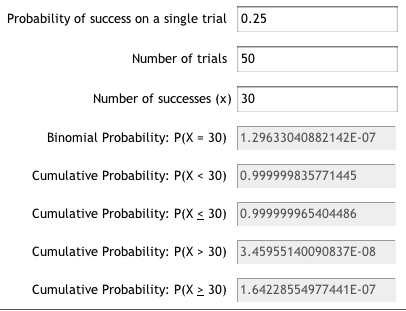
A probability of success of 0.25 assumes there are four answers to choose from. I don’t know whether this is correct and haven’t been able to find out, but it seems feasible.
In fact, an older article says that her scores in the first 771 failed tests were typically between 30% and 50%. With such a sample size, that distribution suggests she might have a little knowledge of the subject.
A straight one-in-three or one-in-four guess would produce a range of results centred around 33% or 25%, so it sounds like it wasn’t complete guesswork but perhaps she wasn’t picking up some of the fundamentals as quickly as she – and other road users – would have liked.
Still, I was intrigued to see how long it would take infinite monkeys to pass this test. Could a Korean zoo actually stand a chance of getting a driving licence?
The bottom number produced by the calculator – P(X≥30) – is the significant one, and it’s miniscule. This is the probability of achieving a passing mark of 60% or higher, purely by picking answers at random.
It equates to odds of greater than six million to one!
And so, if our heroine was indeed just turning up and attacking the test with a ham-fisted crayon, she was running seriously ahead of expectation.
I wonder if we’ll hear more about her exploits the first time she guesses wrong at which pedal is the brake…

See Maths rocks 🙂
You’re missing a trick here though: how many different tests must there be? I doubt if there’s nearly enough to not make it perfectly valid to go in with a formula and adjust based on marks.
So I could go in with “all As” and, assuming I recognise the test again I could do an incredibly elaborate version of Mastermind. I doubt if it would take 950 tests that way, given that I only need 60%.
So here’s a proper challenge: what’s the optimal strategy, assuming N tests? 🙂
The optimal strategy is to learn that red means stop and that motorways are not for picnics. 🙂
c) blow it up with a rear missile